Rotor (mathematics)

A rotor is an n-blade object in geometric algebra, which rotates another n-blade object about a fixed or translated point. They are normally motivated by considering an even number of reflections, which generate rotations (see also the Cartan–Dieudonné theorem). Reflections in geometric algebra are handled via (minus) sandwiching multivectors between a unit vector perpendicular to the hyperplane of reflection. Thus rotors are automatically normalised 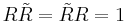. Under a rotation generated by the rotor , a general multivector will transform double-sidedly as 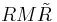. However, as rotors can be combined and follow a group multiplication law, rotors themselves transform single-sidedly under further rotations. This in particular motivates the definition of spinor in geometric algebra as an object that transforms single-sidedly — i.e. spinors are essentially unnormalised rotors.